What’s the Difference between Average and Median?
Hello non-math friends! Yes, you probably already heard about average and median at school or in the news
Does someone try to confuse you by using two words for the same thing? I’ll tell you the difference today 🙂
In mathematics, average and median are different. The average is the sum of the values divided by the number of values, while the median is the central point in a set of values (so there are as many upper values than the lower ones).
As it’s probably not clear enough in two sentences if you have difficulties with this, I will give you more details and also examples in the following parts
The average
Definition
The result you get by adding two or more amounts together and dividing the total by the number of amounts
Cambridge Dictionary
This definition doesn’t help more than my introduction
But I suppose that your problem is not really the average definition, so I’ll move quickly to the following
Usage
The most common type of average is the arithmetic mean
It’s commonly used in countries using numbers for school evaluation, but you can use it in any situations where you want to analyze a set of number (the average price for a flight to Japan, the average size of your children, etc.)
We generally use the average for relatively small sets of values, and only if we know all the values when doing the math
You’ll see later that this is not always the best way to do for other kinds of data
Example
I’ll use again the example of the price for a flight from New-York to Japan
Let’s say that you find three different airlines companies:
- Cathay Pacific: $700
- Asiana: $800
- ANA: $1,300
What’s the average?
Like I wrote earlier, start adding all the values
That’s to say: 800+900+1300, the total is 3000
You now divide the total by the number of values (3)
So 3000/3 is 1000
The average price for this flight is $1,000
The median
Let’s move now to the median, probably less known
Definition
A value in an ordered set of values below and above which there is an equal number of values or which is the arithmetic mean of the two middle values if there is no one middle number
Merriam-Webster
The median is more a statistic term than mathematic
The goal of a median is to find the central point in a set of values
When found, you must have as many upper than lower values
Usage
We generally use the median when the values aren’t evenly distributed
For example, it’s the case for salaries
An average salary doesn’t make sense, the median salary is a better information
For example, if you include unemployed and billionaires, what the real sense of the average?
That’s why the median is better.
The median excludes the extremes, to find the central point.
That is more relevant, mainly for big sets of values
I will show you that in the next example
Example
Here is an example with different values. I will show you the result for average and median on this set
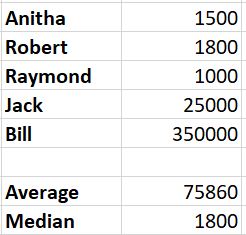
Let’s say we have 5 peoples, here are their salaries:
- Anitha: $1,500
- Robert: $1,800
- Raymond: $1,000
- Jack: $25,000
- Bill: $350,000
I’ll not do the math, as tools like Microsoft Excel allow you to make it directly. You can also use a scientific calculator
(In this case, there is no real calculation to do, but hey I don’t spoil you ^^)
I’ll go directly to the result, and explain it to you just after:
So, I just type the same values in Excel
With the results above, you can see that the average salary is $75,860
But there is no sense, as nobody except Bill get this salary level
So it’s not a good idea of the reality
But the median salary tells us the central point, at $1,800
As the set of values is small, it’s not really a better idea of the situation, but this result is still much closer to reality
We have 2 people over 1800, and 2 under 1800, so it’s exactly what we wanted
Related questions
How to get the median and average in Excel? For the average you have the information displayed directly while selecting a data set (bottom right). And you can also use the functions: AVERAGE() and MEDIAN() to find it
Conclusion
You now know the difference between the average (= arithmetic mean) and the median in mathematic or statistic
It’s important to well remember this difference to not be confused while reading a statistic or an article
I only presented here a quick comparison of these two values
Be aware that there are other variations, and that there are other statistics functions such as standard deviation or variance.
Maybe for another post? 🙂